Gases: são substâncias ou misturas formadas por moléculas em contínuo movimento desordenado, provocando colisões perfeitamente elásticas entre estas moléculas. O estado em que um gás se apresenta é caracterizado por três variáveis de estado: Temperatura, Pressão e Volume.
Podemos referir a esta como o grau de agitação térmico das moléculas no estado gasoso. Em relação aos gases, é mais comum a utilização da temperatura em kelvin (K), portanto, se necessário, devemos transformar a temperatura de Celsius (Tc) para kelvin (Tk) pela equação Tk =Tc + 273.
É o espaço ocupado por uma substância. No caso dos gases, este volume será dado pelo recipiente em que o gás é mantido. As principais unidades de volume e as transformações mais comuns são:
1m³ = 1000 L = 1000 dm³
1 dm³ = 1L = 1000 cm³ = 1000 mL
É a manifestação da colisão das moléculas de um gás contra as paredes do recipiente que o contém. As unidades de pressão mais utilizadas, assim como as transformações entre estas são:
1 atm = 76 cmHg = 760 mmHg = 101,3 kPa
1 mmHg = 1 torr.
Consideremos que um gás sofre uma transformação quando ocorre mudanças nas suas variáveis de estado (V, P, T). Algumas transformações ocorrem mantendo-se uma variável constante, com variação das duas demais variáveis.
Uma determinada massa de gás ocupa um volume inversamente proporcional a pressão exercida sobre este. Assim, para um gás que sofre uma transformação isotérmica, tendo os estados iniciais 1 e estados finais 2, temos: \({{P}_{1}}{{V}_{1}}={{P}_{2}}{{V}_{2}}\).
Mantendo-se o volume de uma amostra de gás constante, a pressão do sistema será diretamente proporcional a temperatura. Assim, numa transformação isovolumétrica do estado 1 a 2, teremos \(\frac{{{V}_{1}}}{{{T}_{1}}}=\frac{{{V}_{2}}}{{{T}_{2}}}\).
Mantendo-se o volume de uma amostra de gás constante, a pressão do sistema será diretamente proporcional a temperatura. Assim, numa transformação isovolumétrica do estado 1 a 2, teremos \(\frac{{{P}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}}{{{T}_{2}}}\).
Considerando uma massa fixa de gás em que as três variáveis de estado se alteram simultaneamente, levando-se em consideração as leis anteriormente expostas, podemos propor que \(\frac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}}\).
Volumes iguais de diferentes gases a mesma T e P são constituídos pelo mesmo número de moléculas.
Baseia-se nas leis anteriormente expostas, em que combinando-se asa equações, temos PV=nRT, onde P=pressão, V=volume, n=número de mols, R=constante universal dos gases e T=temperatura.
Volumes iguais de diferentes gases a mesma T e P são constituídos pelo mesmo número de moléculas.
Uma mistura gasosa é sempre homogênea e o número total de mols de gases é a soma do número de mols de cada um dos gases componentes desta mistura. Assim, pode-se extrapolar as lei geral dos gases e a equação de Clapeyron, considerando apenas que o número de mols é dada por \(\sum{n={{n}_{1}}-{{n}_{2}}+\cdot\cdot \cdot }\)
\[PV=\sum{nRT\,e\,\frac{{{P}_{A}}{{V}_{A}}}{{{T}_{A}}}+\frac{{{P}_{B}}{{V}_{B}}}{{{T}_{B}}}+\,\cdot\cdot \cdot \,=\frac{PV}{T}}\]
A pressão total de uma mistura de gases é dada pela soma das pressões de cada um dos gases componentes, e é proporcional a fração molar (x) do gás na mistura.
\[{{P}_{A}}={{X}_{A}}P;\,{{P}_{B}}={{x}_{B}}P;\cdot\cdot \cdot \,e\,{{x}_{A}}+{{x}_{B}}+\,\cdot \cdot \cdot \,\,=\,1\]
(UEL - PR) Para dada amostra de substância gasosa, quando se dobra a pressão, à temperatura constante, o volume se reduz à metade.
Essa afirmação explicita o que é conhecido como lei de:
(UFRN) Reduzindo-se à metade a pressão exercida sobre 150 cm³ de ar, o novo volume, à temperatura constante, será, em cm³:
(UEM - PR) Assinale o que for correto.
(PUC – RJ) Um pneu de bicicleta é calibrado a uma pressão de 4 atm em um dia frio, à temperatura de 7 °C. Supondo que o volume e a quantidade de gás injetada são os mesmos, qual será a pressão de calibração nos dias em que a temperatura atinge 37 °C?
(UFU – MG) A atmosfera é composta por uma camada de gases que se situam sobre a superfície da Terra. Imediatamente acima do solo, ocorre uma região da atmosfera conhecida como troposfera, na qual ocorrem as nuvens, os ventos e a chuva. Ela tem uma altura aproximada de 10 km, a temperatura no seu topo é cerca de –50 °C e sua pressão é de 0,25 atm. Se um balão resistente a altas pressões, cheio com gás hélio até um volume de 10,0 L, a 1,00 atm e 27,0 °C, é solto, o volume deste balão, quando chegar ao topo da troposfera, será de: Dado: 0 Kelvin = –273 °C
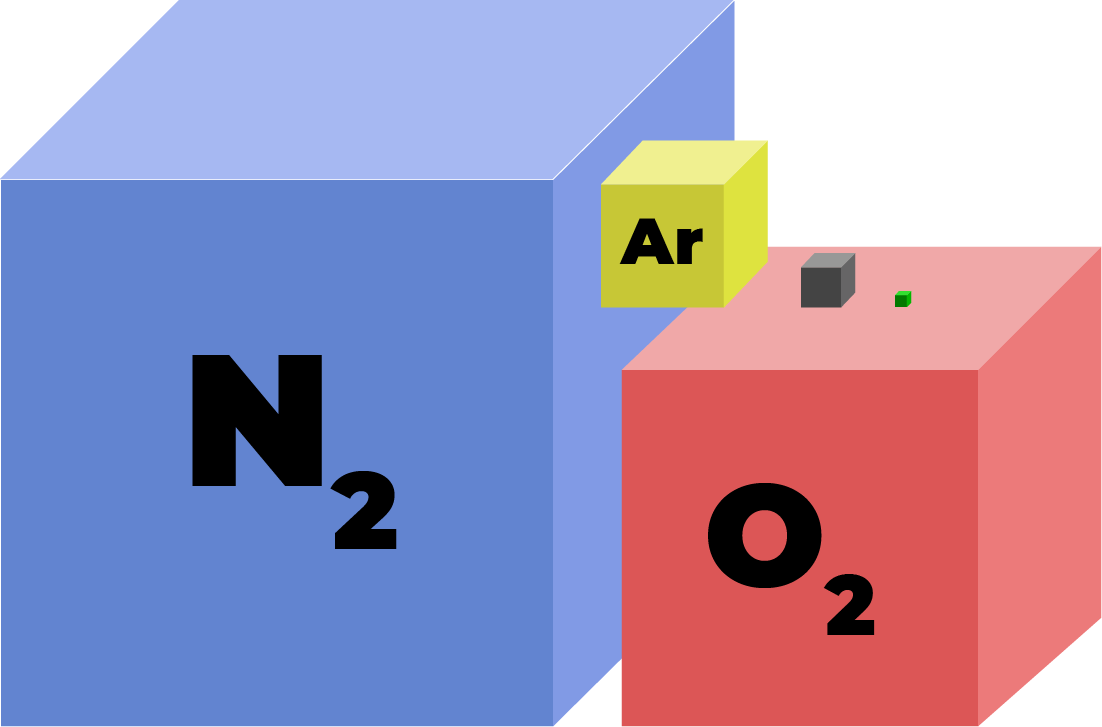
(FATEC – SP) Dois cilindros metálicos iguais contêm gases comprimidos em grau de elevada pureza, sendo que um deles contém 8 m³ de gás nitrogênio, e o outro, 8 m³ de gás hidrogênio. Considerando que os dois cilindros estão armazenados nas mesmas condições ambientais, podemos afirmar que:
Dados: massas atômicas: H = 1,0 e N = 14,0
(MACKENZIE - SP) As 355 g de um certo gás \({{X}_{n}}\) ocupam 112,0 L medidos nas CNTP. Se a massa atômica de X é 35,5 u, então o gás tem fórmula molecular: Dado: Volume molar nas CNTP = 22,4 L/mol.
(UEL - PR) Um balão de vidro de 1 litro, com torneira, aberto ao ar, foi ligado a uma “bomba de vácuo” durante algum tempo. Considerando-se que essa bomba é eficiente para baixar, a 25 °C, a pressão até \({{10}^{4}}mmHg\), após fechar a torneira, quantos mols de oxigênio (\({{O}_{2}}\)) foram retirados do balão? (O que resta de ar no balão é desprezível).
Dados: Volume molar dos gases a 1 atm e 25 °C = 25 L/mol Composição aproximada do ar = 80% de \({{N}_{2}}\) e 20% de \({{O}_{2}}\) (% em mols). Pressão atmosférica = 760 \(mmHg\).
(PUC – RJ) Qual é a pressão exercida pela mistura de 4 g de \({{H}_{2}}\) e 8 g de He (comportando-se como gases ideais) quando a mistura é confinada num recipiente de 4,0 L à temperatura de 27 °C? Dados: \(R=0,082L\cdot atm\cdot mo{{l}^{-1}}\cdot \,{{K}^{-1}};\,\,H=1;\,\,He=4\).
(UNIFENAS) O número total de mols e o volume ocupado por uma mistura de 2,76 g de metano \((C{{H}_{4}})\) e de 9,34 g de amônia \((N{{H}_{3}})\) a 200 °C e 3,00 atm é: Dados: massas atômicas: C = 12, H = 1, N = 14, \(R=0,082L\cdot atm\cdot mo{{l}^{-1}}\cdot {{K}^{-1}}\).
(ITA – SP) A 25 ºC, uma mistura de metano e propano ocupa um volume (V), sob uma pressão total de 0,080 atm. Quando é realizada a combustão completa desta mistura e apenas desta mistura o dióxido de carbono é coletado, verifica-se que a pressão desse gás é de 0,12 atm, quando este ocupa o mesmo volume (V) e está sob a mesma temperatura da mistura original. Admitindo que os gases têm comportamento ideal, assinale a opção que contém o valor correto da concentração, em fração em mols, do gás metano na mistura original.
(PUC – BA) Duas amostras de igual massa de um mesmo gás foram submetidas ao seguinte teste, à temperatura constante:
Os dados obtidos para a pressão e volume das amostras comprovam a lei de:
(FUVEST – SP) Se um certo gás, contido em um compartimento e exercendo pressão de 10 cmHg, for comprimido de maneira a ocupar um vigésimo do seu volume inicial, qual será a pressão final? (temperatura constante)
(UEBA – BA) Um balão-propaganda cheio de gás hélio, ao nível do mar, ocupa um volume de 250 L. Seu volume, após lançamento, numa altitude de 3.000 m será (obs.: admitindo-se que a temperatura tenha se mantido constante):
(UNB – DF) Um balão contendo gás oxigênio (\({{O}_{2}}\)), mantido à pressão constante, tem volume igual a 10 L, a 27 °C. Se o volume for dobrado, poderemos afirmar que:
(UNIRIO – RJ) O uso de amoníaco (\({{NH}_{3}}\)) nos cigarros aumenta o impacto e o efeito da nicotina. (...) com esse estudo confirmamos o que antes desconfiávamos: as empresas manipulam a quantidade de amoníaco com o propósito de reforçar a nicotina, disse o deputado Henry Waxman (E.U.A).
Jornal do Brasil - 31/7/97.
Suponha que uma amostra de cigarro contenha 5 mL de \({{NH}_{3}}\), a 27 °C. Se aquecermos o cigarro a 627 °C, mantendo a pressão constante, o volume de \({{NH}_{3}}\), em L, será de:
(UNESA – RJ) Um volume de 10 L de um gás perfeito teve sua pressão aumentada de 1 para 2 atm e sua temperatura aumentada de –73 °C para + 127 °C. O volume final, em litros, alcançado pelo gás foi de:
(FEI – SP) Uma residência consumiu no ano 2000, entre os meses de janeiro e março, 1,6 kg de gás natural. O volume consumido, em metros cúbicos (m³), medido nas CNTP, considerando o gás natural como metano (\({{CH}_{4}})\) puro, é:
(H = 1, C = 12, volume molar nas CNTP = 22,4 L/mol)
(UFRS – RS) Dois balões indeformáveis (I e II), à mesma temperatura, contêm, respectivamente, 10 L de \({{N}_{2}}\) a 1 atm e 20 L de \(CO\) a 2 atm. Se os dois gases forem reunidos no balão I, a pressão total da mistura será:
(ITA – SP) Dois compartimentos, 1 e 2, têm volumes iguais e estão separados por uma membrana de paládio, permeável apenas à passagem de hidrogênio. (Inicialmente, o compartimento 1 contém hidrogênio puro (gasoso) na pressão \(P({{H}_{2}},puro)\,= 1 atm\), enquanto o compartimento 2 contém uma mistura de hidrogênio e nitrogênio, ambos no estado gasoso, com pressão total \(P(mist)\,=\,(P({{H}_{2}})+({{N}_{2}}))\,=\,1atm\). Após o equilíbrio termodinâmico entre os dois compartimentos ter sido atingido, é CORRETO afirmar que:
(UEM – PR) Um balão fechado e impermeável a gases é preenchido com gás hélio até um volume de 100 L, com pressão interna de 4 atm e temperatura de 27ºC (ao nível do mar). Esse balão, ao ser solto, pode atingir a troposfera, podendo sofrer variações de volume, mas sem estourar (10 km de altura). Considere que, durante a subida, da superfície terrestre até os 10 km de altura, a variação de pressão atmosférica é de –0,075 atm/km e a variação de temperatura é de –8 ºC/km e assinale a(s) alternativa(s) correta(s).
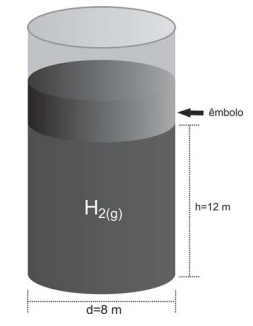
(UEM – PR) O desenho abaixo representa um recipiente cilíndrico que é aberto na parte superior, hermeticamente fechado na parte inferior e vedado com auxílio de um êmbolo que pode ser deslocado verticalmente. O recipiente contém 4g do gás \({{H}_{2}}\) que se encontra a uma temperatura de -73º C.
Considere o \({{H}_{2}}(g)\) um gás ideal e desconsidere a pressão atmosférica e o atrito entre o êmbolo e as paredes do recipiente. Sobre o exposto, assinale o que for correto.
(Dados: constante dos gases = 8,314 \(Pa.{{m}^{3}}\,\,mo{{l}^{-1}}.{{K}^{-1}}\), aceleração da gravidade = 10,0 \(m.{{s}^{-2}}\), π = 3,1.)
(UEM – PR) Considerando os dois principais gases envolvidos no processo de respiração e os dados fornecidos abaixo, assinale o que for correto.
Dados: \(R=0,082\,atm.L.mo{{l}^{-1}}.{{K}^{-1}},\,1atm=760mmHg\)
(UEM – PR) Considerando que os gases mencionados abaixo comportam-se como gases ideais, assinale o que for correto.
Dado: \(R=0,082\,atm.L.mo{{l}^{-1}}.{{K}^{-1}}\).
(UEM – PR) Considerando que todos os gases abaixo se comportam como gases ideais, assinale o que for correto.
(UEM – PR) Assinale o que for correto.
(UEM – PR) Assinale o que for correto.
(EEM – SP) Uma determinada massa gasosa, confinada em um recipiente de volume igual a 6,0 L, está submetida a uma pressão de 2,5 atm e sob temperatura de 27 °C. Quando a pressão é elevada em 0,5 atm, nota-se uma contração no volume de 1,0 L.
(FRB – BA) Um balão meteorológico com 50 L de gás hélio, a 20 ºC e ao nível do mar, é lançado na atmosfera. Ao atingir a estratosfera, a pressão desse gás torna-se 0,4 atm e a temperatura, –50 ºC. Determine, em L, a capacidade que o balão deve ter antes do lançamento.
(FAAP – SP) Um recipiente, munido de um êmbolo móvel, contém 10 L de \({{O}_{2}}\) à pressão de 1 atm. Mantendo-se constante a temperatura por movimentação do êmbolo, pressiona-se o gás até que seu volume seja reduzido para 2 L. Pedem-se:
Você chegou ao fim dessa aula com sucesso!
Selecione o botão avançar para seguir para a próxima aula.